Absolute Value

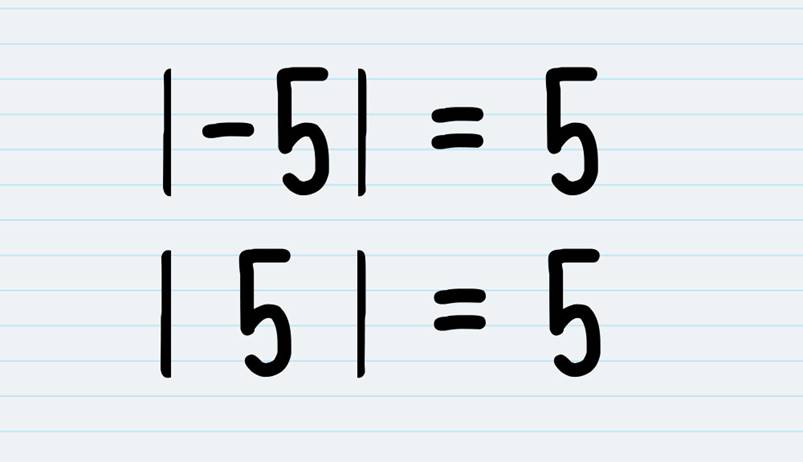
Overview

The absolute value of an integer is the distance the integer is from zero on the number line.

The absolute value symbol is a pair of vertical bars (I I).

Absolute value is always a positive number.

It is the distance the number is from zero on the number line.

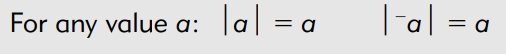
Let’s Practice

Complete the learning activity below.

Absolute Value of a Negative Integer

In mathematics, we often encounter negative numbers, which are less than zero. Negative numbers can sometimes be confusing, especially when determining their distance from zero. That's where the concept of absolute value comes into play. Absolute value helps us find the distance of a number from zero, regardless of whether it is positive or negative.

Let's focus on negative integers and explore how we can find their absolute values. An integer is a whole number that can be positive, negative, or zero. When talking about negative integers, we refer to numbers like -1, -2, -3, and so on.

The absolute value of a negative integer is always a positive number. To understand this, let's consider an example. If we have the number -3, its absolute value would be 3. The absolute value symbol is denoted by vertical bars (| |). So, we write the absolute value of -3 as |-3| = 3.

Here's a rule to remember: when you have a negative integer inside the absolute value symbol, you drop the negative sign and write the number as a positive value.

To find the absolute value of a negative integer, you can follow these steps:

1. Identify the negative integer you want to find the absolute value.

2. Remove the negative sign. Imagine it's not there anymore.

3. Write the number as a positive value.

Look at the example below.

The absolute value of any negative integer is always equal to the numerical value of the number without the sign.

Let's Practice

Complete the learning activity below.

username: vla password: student

Math Games: Absolute Value and Opposing Integers

Absolute Value of a Positive Integer

In mathematics, we often work with positive numbers, which are numbers greater than zero. When we want to find the distance of a positive number from zero, we use the concept of absolute value. Absolute value helps us determine the magnitude or size of a number, regardless of its sign.

Let's focus on positive integers and understand how to find their absolute values. Positive integers are whole numbers like 1, 2, 3, etc.

The absolute value of a positive integer remains the same. In other words, if we have a positive number, its absolute value will also be positive. For example, if we consider the number 4, its absolute value would be 4. We write the absolute value of 4 as |4| = 4.

You don't need to change the number to find the absolute value of a positive integer since it is already positive. The absolute value of a positive integer is the number itself.

Remember that vertical bars (| |) denote the absolute value symbol. So, when you see the absolute value symbol, you know that the result will be a positive number.

Look at the example below.

The absolute value of positive three represents 3 units above zero. The absolute value of any positive integer is always equal to the numerical value of the number without the sign.

The absolute value of any positive or negative integer is the number written without the positive or negative sign.

Let's Practice

Complete the learning activity below.

username: vla password: student

Math Games: Absolute Value of Rational Numbers